
Alright everypony. I gathered everyone so we can all be on the same page about what groups are. Here on this table, I've placed a little plate with a triangle that fits perfectly in it. Can any of you show me some other way I could've placed this triangle?
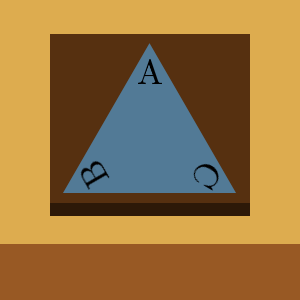

Uhhh, lemme guess. You could rotate it once?

Exactly! The triangle can be rotated once, and it'll still fit in the plate!

And... I suppose you could rotate it twice that. But ain't that pretty much it?

Great thinking! However, there's still something else we can do. Try to think outside the b-

Oh, oh! We can flip it!!

Nice one Pinkie! That's right! We can flip it around the $\text{A}$ axis!

And... we can also flip it around the... $\text{B}$ axis as well?

And don't forget the $\text{C}$ axis, darling.

Great stuff! There's 5 different ways to move the triangle in a way that it still fits in the plate! One way to write this down without needing a physical triangle like we do, is the following notation: $$\triangle \text{ABC}$$ where the first letter represents the top corner, the second letter represents the left corner, and the third letter represents the right corner. So for example, if you look at the triangle when we rotate it once, $\text{A}$ goes to $\text{B}$, $\text{B}$ goes to $\text{C}$, and $\text{C}$ goes to $\text{A}$. So we could say $$\triangle \text{ABC} \ \ \underrightarrow{\text{rotating once}} \ \ \triangle \text{BCA} $$

So... When you rotate it twice, $\text{A}$ goes to $\text{C}$ was, $\text{B}$ goes to where $\text{A}$ was, and so on. $$\triangle \text{ABC} \ \ \underrightarrow{\text{rotating twice}} \ \ \triangle \text{CAB} $$

Pretty much! And when we flip it, all we're doing is swapping two corners. So when we flipped around the $\text{A}$ axis, we just swapped $\text{B}$ and $\text{C}$! $$\triangle \text{ABC} \ \ \underrightarrow{\text{flipping around A}} \ \ \triangle \text{ACB} $$

Okay, we get it. Same thing for the other ones. $$\triangle \text{ABC} \ \ \underrightarrow{\text{flipping around B}} \ \ \triangle \text{CBA} $$ $$\triangle \text{ABC} \ \ \underrightarrow{\text{flipping around C}} \ \ \triangle \text{BAC} $$ Why are we doing this?

Glad you asked! Now we do something completely different. Does any of you know what a permutation is?

Oh! It's when we put things on a line! And we can arrange them in different ways!! Like if we were all on a line we could have me first, then you second, then Applejack third, but we could've done Applejack first, and I could be last! Or, or, I could be second and-

Okay, I think we got it.

Following Pinkie's definition, suppose we have three letters, A, B, and C. And we wish to write them in some order. What are the possible ways we can write those three letters?

Seems like a simple task, darling. $$\text{ABC}\ \ \ \ \text{ACB}\ \ \ \ \text{BAC} \ \ \ \ \text{BCA}\ \ \ \ \text{CAB}\ \ \ \ \text{CBA}$$ There are six total ways to arrange them in unique ways.

Mmmhm, this is where this gets exciting!! Does anypony see the pattern?

Uhm... is it... each arrangement corresponds to one of the ways we moved the triangle?

Yes!! Although both of those things are different in nature, they both share a connection which lets us pair them up like this! $$ \begin{alignat*}{2} \text{ACB} &&& \leftrightarrow \text{flipping around A} \\ \text{BAC} &&& \leftrightarrow \text{flipping around C} \\ \text{BCA} &&& \leftrightarrow \text{rotating once} \\ \text{CAB} &&& \leftrightarrow \text{rotating twice} \\ \text{CBA} &&& \leftrightarrow \text{flipping around B} \end{alignat*} $$ These two operations, along with their elements (be the corners of a triangle or three letters aligned in some order), are what we call a group. Group theory is a part of mathematics that abstracts these operations and treats them in a more general way.

Okay, you lost me at... theory.

Okay, think of it this way. If I have three apples in a basket, and I add two more apples in it, I'll have a total of five apples.

I can certify that math is correct.

If I have instead 3 oranges in a basket, and I add 2 oranges, I'll have 5 oranges in total.

Granted, that's an inferior basket.

My point is, it doesn't matter if we're talking about apples or oranges. Deep down, what maths tells us is that $$3 + 2 = 5$$ And we can choose to interpret these numbers in any way we want. In the same way that numbers are abstractions over amounts of things, groups are abstractions over these kinds of symmetrical operations.